blog
一些简单的markdown 示例
一些数学上标
$\vec{a}$ 向量
$\overline{a}$ 平均值
$\widehat{a}$ (线性回归,直线方程) y尖
$\widetilde{a}$ 颚化符号 等价无穷小
$\dot{a}$ 一阶导数
$\ddot{a}$ 二阶导数
常用数学符号和希腊字母
| 大写 | markdown | 小写 | markdown |
|---|---|---|---|
| $A$ | A | $\alpha$ | \alpha |
| $B$ | B | $\beta$ | \beta |
| $\Gamma$ | \Gamma | $\gamma$ | \gamma |
| $\Delta$ | \Delta | $\delta$ | \delta |
| $E$ | E | $\epsilon$ | \epsilon |
| $\varepsilon$ | \varepsilon | ||
| $Z$ | Z | $\zeta$ | \zeta |
| $H$ | H | $\eta$ | \eta |
| $\Theta$ | \Theta | $\theta$ | \theta |
| $I$ | I | $\iota$ | \iota |
| $K$ | K | $\kappa$ | \kappa |
| $\Lambda$ | \Lambda | $\lambda$ | \lambda |
| $M$ | M | $\mu$ | \mu |
| $N$ | N | $\nu$ | \nu |
| $\Xi$ | \Xi | $\xi$ | \xi |
| $O$ | O | $\omicron$ | \omicron |
| $\Pi$ | \Pi | $\pi$ | \pi |
| $P$ | P | $\rho$ | \rho |
| $\Sigma$ | \Sigma | $\sigma$ | \sigma |
| $T$ | T | $\tau$ | \tau |
| $\Upsilon$ | \Upsilon | $\upsilon$ | \upsilon |
| $\Phi$ | \Phi | $\phi$ | \phi |
| $\varphi$ | \varphi | ||
| $X$ | X | $\chi$ | \chi |
| $\Psi$ | \Psi | $\psi$ | \psi |
| $\Omega$ | \Omega | $\omega$ | \omega |
数学运算符号

关系运算符号

标点符号
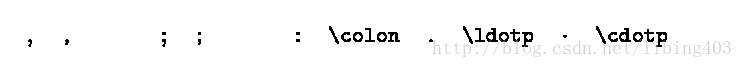
杂项符号

可变大小符号
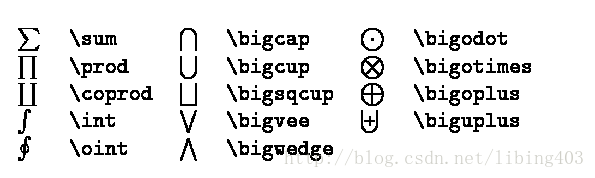
三角函数符号

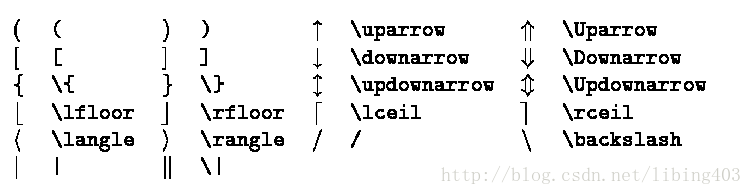
分隔符号
大分割符号
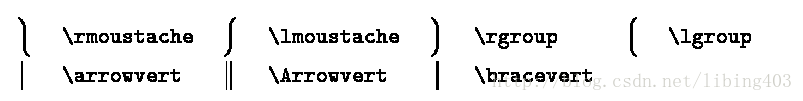
数学读音符号
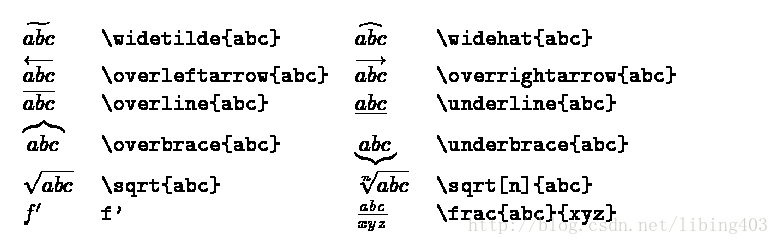
一些例子
\[J_\alpha(x) = \sum_{m=0}^\infty \frac{(-1)^m}{m! \Gamma (m + \alpha + 1)} {\left({ \frac{x}{2} }\right)}^{2m + \alpha} \text {,独立公式示例}\] \[f(n)= \begin{cases} n/2, & \text {if $n$ is even} \\ 3n+1, & \text{if $n$ is odd} \end{cases}\] \[\sum_{i=1}^n \frac{1}{i^2} \quad and \quad \prod_{i=1}^n \frac{1}{i^2} \quad and \quad \bigcup_{i=1}^{2} R\] \[f(x,y,z) = 3y^2z \left( 3+\frac{7x+5}{1+y^2} \right)\]$J_\alpha(x) = \sum_{m=0}^\infty \frac{(-1)^m}{m! \Gamma (m + \alpha + 1)} {\left({ \frac{x}{2} }\right)}^{2m + \alpha} \text {,行内公式示例}$